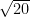Bài1. Hệ thức trong tam giác vuông

–o0o–

1. Khái niệm :

 Cho tam giác ABC vuông tại A . có :

Cạnh huyền : BC.

Cạnh góc vuông : AC, AB.

Đường cao : AH

Hình chiếu :

• BH là hình chiếu của AB lên cạnh huyền BC.
• CH là hình chiếu của AC lên cạnh huyền BC.

2. Các hệ thức :

1.    Định lí 0 : (Pitago)

BC² = AB² + AC²

2.    Định lí 1 :

AB² =BC. BH

AC² =BC. CH

3.    Định lí 2 :

AH² = BH.CH

4.    Định lí 3 :

AB.AC = BC.AH

5.    Định lí 4 :

1/AH² = 1/AB² + 1/AC²

====================================================================

BÀI TẬP SGK

BÀI 1 TRANG 68 : tính x ,y trong các hình sau

Đặt hai cạnh góc vuông : AB = 6; AC =8

Tính hai hình chiếu : x = BH; y = CH

Nhận xét :

•  Cho biết hai cạnh góc vuông, tính hình chiếu
• Theo các hệ thức liên quan hình chiếu phải có cạnh huyền và cạnh góc vuông.
• Do đó, ta Tính  cạnh huyền trước.

Giải.

Xét tam giác ABC vuông tại A, ta có :

Định lí Pitago :

BC² = AB² + AC² = 62 + 8² = 100

= > BC = 

Theo hệ thức :

AB² =BC. BH  <=> 6² = 10.BH = > BH = 36/10 = 3,6

AC² =BC. CH<=> 8² = 10.CH = > BH = 64/10 = 6,4

Hình b :

Đặt cạnh góc vuông : AB = 12

Cạnh huyền : BC = 20

Tính hai hình chiếu : x = BH; y = CH

Giải

Xét tam giác ABC vuông tại A, Theo hệ thức :

AB² =BC. BH  <=> 12² = 20.x

= > x = 144/20 = 7,2

BC = BH + CH <=> 20 = 7,2 + y => y = 20 – 7,2 = 12,8

BÀI 4 TRANG 69 :

Đặt đường cao : AH = 12

hình chiếu : BH = 1

Tính hình chiếu : x = CH;

cạnh góc vuông : y = CH

Giải.

Xét tam giác ABC vuông tại A, Theo hệ thức :

AH² = BH.CH <=> 2² = 1.x => x = 4

Xét tam giác AHC vuông tại H, theo định lí Pitago :

AC² = AH² + CH² ó y2 = 2² + 4² = 20 => y = 

Xem tiếp »