Home » TOÁN HỌC 10 » TOÁN HỌC 12 » GIẢI PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH VÔ TỈ BẰNG PHƯƠNG PHÁP SỬ DỤNG BIỂU THỨC LIÊN HỢP

GIẢI PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH VÔ TỈ BẰNG PHƯƠNG PHÁP SỬ DỤNG BIỂU THỨC LIÊN HỢP

, Bình luận

GIẢI PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH VÔ TỈ BẰNG PHƯƠNG PHÁP  SỬ DỤNG BIỂU THỨC LIÊN HỢP 1. Định nghĩa về nghiệm của phương trình:   ...

GIẢI PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH VÔ TỈ
BẰNG PHƯƠNG PHÁP  SỬ DỤNG BIỂU THỨC LIÊN HỢP

1. Định nghĩa về nghiệm của phương trình:
     Cho hàm số 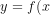 xác định trên . Giá trị  thỏa  được gọi là nghiệm của phương trình  trên .
2. Định lí Bơzu: Nếu đa thức hệ số thực  có nghiệm  thì ta có phân tích  với  là một đa thức hệ số thực.
3. Cơ sở phương pháp liên hợp
  Giả sử ta cần giải phương trình  và đã biết trước được một nghiệm .
     Khi đó ta tìm cách phân tích đưa phương trình  về dạng 
 Để phân tích được về thừa số  ta chuyển các biểu thức vô tỉ về các đa thức. Chẳng hạn trong phương trình có hạng tử  thì ta ghép với  ta được .
  Để thuận lợi trong việc phân tích ta cần nắm vững các hằng đẳng thức
          
          
          ……………………………….
          .
Ví dụ 1. Giải phương trình
.
Lời giải.
Điều kiện: .
Nhận thấy phương trình đã cho có nghiệm  nên ta biến đổi phương trình đã cho như sau
Vì
 nên (*) vô nghiệm.
Vậy .
Nhận xét: Trong lời giải trên có hai mẫu chốt quan trọng là:
 Nhẩm trước 1 nghiệm của phương trình. Khi nhẩm nghiệm ta thường ưu tiến các giá trị của để các biểu thức dưới dấu căn nhân giá trị là một luỹ thừa tương ứng với bậc của căn.
 Dùng lượng liên hợp để tạo ra nhân tử . Ở đây ta thường thêm bớt các hạng tử phù hợp để tạo ra thừa số chung. Trong bài trên với  thì  nên ta ghép  và .

Ví dụ 2. Giải phương trình
.
Lời giải.
Điều kiện: .
Phương trình tương đương với
.
+) Nếu  thì ta thấy (*) vô nghiệm
+) Xét , khi đó
Do đó
 nên (*) vô nghiệm.
Vậy .
Ví dụ 3. Giải bất phương trình
.
Lời giải.
Bất phương trình đã cho tương đương với
Với 
            .
Dấu “=” xảy ra khi .
Nên .
Vậy .
Ví dụ 4. Giải phương trình :
.
Lời giải.
Nhận thấy phương trình có nghiệm  nên ta biến đổi như sau
Từ (*) và phương trình đề bài ta suy ra
Đặt , ta có:
.
Thử lại ta thấy  không thoả phương trình.
Vậy .
Ví dụ 5. Giải phương trình:
.
Lời giải.
Điều kiện: .
Ta thấy phương trình  có hai nghiệm . Mà hai nghiệm này là nghiệm của tam thức  nên ta tìm cách tạo ra thừa số . Ta biến đổi phương trình đã cho như sau:
.
Kết hợp điều kiện ta có nghiệm của bất phương trình là:
.

Luyện thi An Dương

Luyện thi kiến thức Toán Phổ Thông - Đại học. Đồng thời có các chuyên đề , định hướng về hướng nghiệp - kỹ năng sống.

Có thể bạn quan tâm

Có 0 nhận xét Đăng nhận xét

Copyright © 2016 Luyện thi An Dương
Thiết kế bởi Luyện thi An Dương