Để lập phương trình mặt phẳng ) , ta có các cách sau:
, ta có các cách sau:
Cách 1: Tìm một điểm ) mà mặt phẳn g
mà mặt phẳn g ) đi qua và một VTPT
đi qua và một VTPT ) . Khi đó phương trình của
. Khi đó phương trình của ) có dạng:
có dạng:
Một số lưu ý khi tìm VTPT của mặt phẳng ) :
:
Cách 2: Giả sử phương trình ) có dạng:
có dạng:  với
với  .
.
Dựa vào giả thiết của đề bài ta tìm được ba trong bốn ẩn  theo ẩn còn lại. Chẳng hạn
theo ẩn còn lại. Chẳng hạn  . Khi đó phương trình
. Khi đó phương trình ) là:
là:  .
.
Chú ý: Nếu mặt phẳng ) đi qua
đi qua ) thì phương trình của
thì phương trình của ) có dạng:
có dạng:
Ví dụ 1. Lập phương trình mặt phẳng ) , biết:
, biết:
1) ) đi qua ba điểm
đi qua ba điểm ,B(2;-1;3),C(-1;2;-1)) ,
,
2) ) đi qua hai điểm
đi qua hai điểm  và song song với
và song song với  ,
,
3) ) đi qua
đi qua ) , vuông góc với
, vuông góc với :2x-y+z-1=0) và song song với
và song song với  ,
,
4) ) vuông góc với hai mặt phẳng
vuông góc với hai mặt phẳng :x+y+z-1=0) ,
, :2x-y+3z-4=0) và khoảng cách từ
và khoảng cách từ  đến
đến ) bằng
bằng  .
.
Lời giải.
1) Ta có ,\text{%20}\overrightarrow{AC}=(-2;1;-2)) , suy ra
, suy ra )
Phương trình :2x-2y-3z+3=0) .
.
2) Ta có ) , suy ra
, suy ra )
Vì ) đi qua
đi qua  và song song với
và song song với  nên
nên ) nhận
nhận ) làm VTPT.
làm VTPT.
Suy ra phương trình :2x+y-3=0) .
.
3) Ta có: 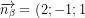,\text{%20}\overrightarrow{{{u}_{\Delta%20}}}=(2;1;-3))
Do \bot%20(\beta%20)%20\\%20&%20(\alpha%20)//\Delta%20\\%20\end{matrix}%20\right.\Rightarrow%20\overrightarrow{{{n}_{\alpha%20}}}=\overrightarrow{{{n}_{\beta%20}}}\wedge%20\overrightarrow{{{u}_{\Delta%20}}}=(2;8;4)) .
.
Phương trình :x+4y+2z-7=0) .
.
4) Ta có ,\text{%20}\overrightarrow{{{n}_{2}}}=(2;-1;3)) lần lượt là VTPT của
lần lượt là VTPT của ) và
và ) .
.
Vì ) vuông góc với hai mặt phẳng
vuông góc với hai mặt phẳng ) và
và ) nên
nên ) nhận véc tơ
nhận véc tơ
Suy ra phương trình ) có dạng
có dạng  .
.
Mặt khác : )=\sqrt{26}) nên ta có:
nên ta có:  .
.
Vậy phương trình :4x-y-3z\pm%2026=0) .
.
Ví dụ 2. Lập phương trình mặt phẳng ) , biết :
, biết :
1) ) đi qua giao tuyến của hai mặt phẳng
đi qua giao tuyến của hai mặt phẳng :x-3z-2=0) ;
; :y-2z+1=0) và khoảng cách từ
và khoảng cách từ ) đến
đến ) bằng
bằng  .
.
2) ) đi qua hai điểm
đi qua hai điểm ,B\left(%20-2;1;3%20\right)) sao cho khoảng cách từ
sao cho khoảng cách từ ) đến
đến ) bằng khoảng cách từ
bằng khoảng cách từ ) đến
đến ) .
.
Lời giải.
1) Giả sử :ax+by+cz+d=0) .
.
Ta có ,B(5;1;1)) là điểm chung của
là điểm chung của ) và
và )
Vì ) đi qua giao tuyến của hai mặt phẳng
đi qua giao tuyến của hai mặt phẳng ) và
và ) nên
nên )
Suy ra  .
.
Mặt khác: %20\right)=\frac{7}{6\sqrt{3}}\Rightarrow%20\frac{\left|%20\frac{1}{2}c+d%20\right|}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}=\frac{7}{6\sqrt{3}})
2) Giả sử :ax+by+cz+d=0)
Vì \Rightarrow%20\left\{%20\begin{matrix}%20&%20a+2b+c+d=0%20\\%20&%20-2a+b+3c+d=0%20\\%20\end{matrix}%20\right.\Leftrightarrow%20\left\{%20\begin{matrix}%20&%20a=\frac{-b+2c}{3}%20\\%20&%20d=-\frac{5b+5c}{3}%20\\%20\end{matrix}%20\right.)
Mặt khác: %20\right)=d\left(%20D,(P)%20\right)\Leftrightarrow%20\left|%202a-b+c+d%20\right|=\left|%203b+c+d%20\right|)
Ví dụ 2. Trong không gian Oxyz cho điểm ) và hai đường
và hai đường
1) Viết phương trình mặt phẳng (P) đi qua A và  ,
,
2) Chứng minh rằng  và
và  cắt nhau. Viết phương trình mặt phẳng (Q) chứa
cắt nhau. Viết phương trình mặt phẳng (Q) chứa  và
và  .
.
Lời giải.
Ta có: Đường thẳng  đi qua
đi qua ) , VTCP
, VTCP )
Đường thẳng  đi qua
đi qua ) , VTCP
, VTCP )
1) Ta có: )
Do (P) đi qua A và  nên
nên )
Suy ra phương trình :4x-5y+3z-3=0) .
.
2) Xét hệ phương trình 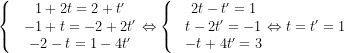
Suy ra  và
và  cắt nhau tại
cắt nhau tại ) .
.
Ta có )
Phương trình (Q):  .
.
Ví dụ 3. Trong không gian Oxyz cho ba đường thẳng
Viết phương trình mặt phẳng ) đi qua
đi qua  và cắt
và cắt  lần lượt tại A,B sao cho
lần lượt tại A,B sao cho  .
.
Lời giải.
Ta có ) ,
, )
Suy ra ;a+2b-2)) , đặt
, đặt 
Từ 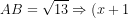}^{2}}+4{{x}^{2}}+{{(x-2)}^{2}}=13\Leftrightarrow%20x=-1,x=\frac{4}{3})
Suy ra ) là VTPT của
là VTPT của ) .
.
Phương trình :7x-6y-4z+13=0) .
.
Suy ra ) là VTPT của
là VTPT của ) .
.
Phương trình :14x-11y-5z-25=0) .
.

Có 0 nhận xét Đăng nhận xét