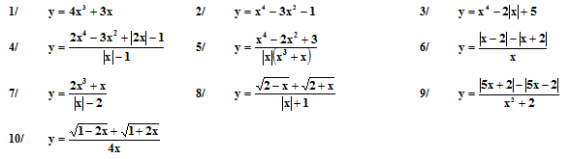Hiển thị các bài đăng có nhãn TOÁN HỌC 10. Hiển thị tất cả bài đăng
Home
»
Bài viết cho "
TOÁN HỌC 10
"
Bất đẳng thức Cauchy-Bunhiacopxkii-Schwarz cho các số thực và ứng dụng trong chương trình phổ thông
Cho $a = \left( {{a_1},a_2...,{a_n}} \right)$ và $b = \left( {{b_1},{b_2},...,{b_n}} \right)$ là hai bộ số thực. Khi ấy ta có
$$ (a_1^2+a_2^2+...+a_n^2)(b_1^2+b_2^2+...+b_n^2) \ge (a_1b_1+a_2b_2+...+a_nb_n)^2 \ \ \ (1.1)$$
Dấu bằng xảy ra khi và chỉ khi $a$ và $b$ tỉ lệ, nghĩa là tồn tại hằng số $r$ sao cho ${a_i} = r{b_i}$ với mọi $i \in \{ 1,2,...,n\} .$
Trong chương trình toán phổ thông, bất đẳng thức Cauchy-Bunhiacopxkii-Schwarz thường được phát biểu khi $n=2$ và mở rộng cho $n=3$. Bất đẳng thức này được ứng dụng trong bài toán chứng minh bất đẳng thức, bài toán tìm giá trị lớn nhất, giá trị nhỏ nhất, giải phương trình, bất phương trình và hệ đại số...
Ví dụ 1.1
Hai số dương $x,y$ thỏa mãn $3x+2y=6xy$. Tìm giá trị nhỏ nhất của tổng $x+y$.
Giải: Nhận xét rằng $3x+2y=6xy$ khi và chỉ khi $ \dfrac{2}{x}+\dfrac{3}{y}=6$ và $$\sqrt{2}+\sqrt{3}=\sqrt{\dfrac{2}{x}}.\sqrt{x}+\sqrt{\dfrac{3}{y}}.\sqrt{y}$$
Áp dụng bất đẳng thức Cauchy-Bunhiacopxkii-Schwarz với $n=2$, ta được
$$(\sqrt{2}+\sqrt{3} )^2 \le \left( \dfrac{2}{x}+\dfrac{3}{y}\right)(x+y)=6(x+y).$$
Suy ra $$x+y \ge \dfrac{1}{6}(\sqrt{2}+\sqrt{3} )^2 =\dfrac{5+2\sqrt{6}}{6}.$$
Vậy giá trị nhỏ nhất của tổng $x+y$ bằng $\dfrac{5+2\sqrt{6}}{6}$ đạt được khi
$$ \dfrac{2}{x}+\dfrac{3}{y}=6$$ và
$$\dfrac{x}{\dfrac{2}{x}}=\dfrac{y}{\dfrac{3}{y}}$$. Điều này tương đương với
$$ x=\dfrac{2+\sqrt{6}}{6}$$
và $$ x=\dfrac{3+\sqrt{6}}{6}.$$
Ví dụ 1.2:
Giải bất phương trình $\sqrt{x-1}-\sqrt{2x^2-10x+16} \ge 3-x.$
Giải: Ta biến đổi phương trình về dạng $\sqrt{x-1}+x-3 \ge\sqrt{2x^2-10x+16}.$
Sử dụng bất đẳng thức Cauchy-Bunhiacopxkii-Schwarz với $n=2$, ta được
$$ \sqrt{2[(x-1)+(x-3)^2]} \le \sqrt{x-1}+x-3.$$
Vậy bất phương trình tương đương với dấu "=" xảy ra, tức là
$$\sqrt{x-1}=x-3\Leftrightarrow x^2-7x+10=0.$$
Giải phương trình cuối ta được $x=2$ và $x=5$. Vậy bất phương trình có nghiệm $x=2$ và $x=5$.
Ví dụ 1.3:
Cho $a,b,c$ là ba cạnh của tam giác. Chứng minh bất đẳng thức sau:
$$\sqrt{3(\sqrt{ab}+\sqrt{bc}+\sqrt{ac} )} \ge \sqrt{a+b-c} + \sqrt{b+c-a}+ \sqrt{c+a-b}.$$
Giải: Lấy $x,y,z>0$ và đặt $a=x+y, b=y+z, c=x+z$. Khi đó bất đẳng thức đã cho tương đương với bất đẳng thức
$$3 \sum\limits_{cyc} \sqrt{(x+y)(y+z)} \ge 2 \left(\sum\limits_{cyc} \sqrt{x} \right)^2. $$
Từ bất đẳng thức Cauchy-Bunhiacopxkii-Schwarz ta có
$$
3 \sum\limits_{cyc} \sqrt{(x+y)(y+z)} \ge 3 \sum\limits_{cyc} (y +\sqrt{xz}) \\
\ge 2 \sum\limits_{cyc} y + \sum\limits_{cyc} \sqrt{xz} \\
= 2 \left(\sum\limits_{cyc} \sqrt{x} \right)^2.
$$
Bất đẳng thức Cauchy-Bunhiacopxkii-Schwarz được sử dụng rất nhiều trong việc chứng minh các bất đẳng thức. Đặc biệt trong các bài thi chọn học sinh giỏi, thi Olympic.
Ví dụ 1.4:
Cho các số dương $a,b,c$ thỏa mãn
$$\dfrac{1}{a+b+1} +\dfrac{1}{b+c+1}+\dfrac{1}{c+a+1} \ge 1.$$
Chứng minh rằng
$$a+b+c \ge ab+bc+ca.$$
(Andrei Ciupan, Chọn đội tuyển Romania dự thi Junior BMO 2007)
Giải:\\
Cách 1: Áp dụng bất đẳng thức Cauchy-Bunhiacopxkii-Schwarz, dễ thấy
$$(a+b+1)(a+b+c^2)\ge (a+b+c)^2.$$
Từ đó dẫn đến
$$
1 \le \dfrac{1}{a+b+1}+\dfrac{1}{b+c+1}+\dfrac{1}{c+a+1}
\le \dfrac{a+b+c^2}{(a+b+c)^2}+\dfrac{b+c+a^2}{(a+b+c)^2}\dfrac{c+a+b^2}{(a+b+c)^2}.
$$
Suy ra
$$(a+b+c)^2 \le 2(a+b+c)+a^2+b^2+c^2,$$
tức là
$$a+b+c \ge ab+bc+ca.$$
Bất đẳng thức của ta được chứng minh xong. Đẳng thức xảy ra khi và chỉ khi $a=b=c=1.$
Cách 2: Từ giả thiết sử dụng bất đẳng thức Cauchy-Bunhiacopxkii-Schwarz, ta có
$$
2 \ge \left( 1- \dfrac{1}{a+b+1} \right) + \left( 1- \dfrac{1}{b+c+1} \right)+ \left( 1- \dfrac{1}{c+a+1} \right)\\
=\dfrac{a+b}{a+b+1}+\dfrac{b+c}{b+c+1}+\dfrac{c+a}{c+a+1}\\
\ge \dfrac{[(a+b)+(b+c)+(c+a)]^2}{(a+b)(a+b+1)+(b+c)(b+c+1)+(c+a)(c+a+1)}\\
=\dfrac{2(a^2+b^2+c^2) +4 (ab+bc+ca)}{(a^2+b^2+c^2) +(ab+bc+ca)+(a+b+c)}.
$$
Từ đây ta suy ra được
$$(a^2+b^2+c^2)+(ab+bc+ca)+(a+b+c) \ge (a^2+b^2+c^2)+2(ab+bc+ca),$$
tức là
$$a+b+c \ge ab+bc+ca.$$
Đây chính là điều phải chứng minh.
Ứng dụng của bất đẳng thức giữa trung bình cộng và trung bình nhân trong chương trình toán phổ thông
Bài này là bài kế tiếp của bài:"Bất đẳng thức giữa trung bình cộng và trung bình nhân"
Bất đẳng thức
$$\dfrac{a+b}{2} \, \geq \, \sqrt{ab}.$$
trong chương trình học phổ thông được biết đến với tên gọi bất đẳng thức giữa trung bình cộng và trung bình nhân. Bất đẳng thức này có nhiều ứng dụng vào các bài toán chứng minh bất đẳng thức, bài toán tìm giá trị lớn nhất, giá trị nhỏ nhất, bài toán giải phương trình, bất phương trình.
Sau đây chúng tôi nêu ra một vài ý nghĩa của bất đẳng thức giữa trung bình cộng và trung bình nhân như sau:
Giả sử ta có một tập các hình chữ nhật có diện tích $A$ và độ dài cạnh là $x, y.$ Vì $A=xy$, nên
bất đẳng thức $\dfrac{x+y}{2}\ge \sqrt{xy}$ có ý nghĩa là hình vuông có độ dài cạnh $\sqrt{xy}$ phải có chu vi nhỏ nhất trong số các hình chữ nhật có cùng diện tích $A$. Nói cách khác, trong số tất cả các hình chữ nhật có chu vi $p$ thì hình vuông có cạnh $p/4$ là hình vuông có diện tích lớn nhất.
Một ý nghĩa hình học nữa liên quan đến trung bình cộng và trung bình nhân là coi $\dfrac{1}{2}(x+y)$
là bán kính của một đường tròn và $\sqrt{xy}$ là đường cao xuất phát từ đỉnh góc vuông chắn nửa
đường tròn.
Ví dụ :
Từ một mảnh giấy bìa có dạng hình chữ nhật kích thước $15 \times 8 \ cm$, người ta cắt ra từ bốn góc của hình chữ nhật bốn hình vuông bằng nhau. Mảnh giấy còn lại trông giống như một chữ thập, được gấp làm một cái hộp (không nắp). Hỏi rằng cạnh của bốn hình vuông bằng bao nhiêu để thể tích của chiếc hộp thu được là lớn nhất.
Giải: Gọi $x$ là độ dài cạnh của hình vuông. Khi đó chiếc hộp sẽ có kích thước là $15-x-x; 8-x-x$ và $x$. Thể tích của chiếc hộp là $V$ được tính theo $x$ như sau
$$V = x(15-2x)(8-2x).$$
Ta cần tìm $x$ sao cho $V$ đạt giá trị lớn nhất. Khi chưa có công cụ đạo hàm, ta vẫn có thể tìm
giá trị lớn nhất của $V$ bằng cách sử dụng bất đẳng thức giữa trung bình cộng và trung bình
nhân.
Thực vậy, ta cần phải tìm $k,l$ trong $kx(15-2x)l(8-2x)$ sao cho
$$15-2x=l(8-2x)=kx,$$ và $$2+2l-k=0.$$
Từ đây, biểu diễn $x$ theo $k,l$ ta tìm $k,l$ bằng cách giải hệ phương trình
$$\dfrac{15-8l}{2(1-l)}=\dfrac{8l}{k+2l}$$
hay $2+2l-k=0.$
Giải hệ này cho ta $l=\dfrac{5}{2}, k = 7$. Bây giờ ta áp dụng bất đẳng thức giữa trung bình cộng và
trung bình nhân cho ba số,
$$
V=x(15-2x)(8-2x)=\dfrac{2}{35}.7x (15-2x)(20-5x)
\le \dfrac{2}{35} \left( \dfrac{7x+15-2x+20-5x}{3}\right)^3.
$$
Từ đó,
$$V \le \dfrac{2}{35}. \left(\dfrac{35}{3}\right)^3=\dfrac{2450}{27}.$$
Đẳng thức xảy ra khi và chỉ khi
$$7x=15-2x=20-5x.$$
Giải hệ phương trình này cho ta $x=\dfrac{5}{3}$. Vậy cạnh hình vuông là $\dfrac{5}{3}$ cm.
Bất đẳng thức
$$\dfrac{a+b}{2} \, \geq \, \sqrt{ab}.$$
trong chương trình học phổ thông được biết đến với tên gọi bất đẳng thức giữa trung bình cộng và trung bình nhân. Bất đẳng thức này có nhiều ứng dụng vào các bài toán chứng minh bất đẳng thức, bài toán tìm giá trị lớn nhất, giá trị nhỏ nhất, bài toán giải phương trình, bất phương trình.
Sau đây chúng tôi nêu ra một vài ý nghĩa của bất đẳng thức giữa trung bình cộng và trung bình nhân như sau:
Giả sử ta có một tập các hình chữ nhật có diện tích $A$ và độ dài cạnh là $x, y.$ Vì $A=xy$, nên
bất đẳng thức $\dfrac{x+y}{2}\ge \sqrt{xy}$ có ý nghĩa là hình vuông có độ dài cạnh $\sqrt{xy}$ phải có chu vi nhỏ nhất trong số các hình chữ nhật có cùng diện tích $A$. Nói cách khác, trong số tất cả các hình chữ nhật có chu vi $p$ thì hình vuông có cạnh $p/4$ là hình vuông có diện tích lớn nhất.
Một ý nghĩa hình học nữa liên quan đến trung bình cộng và trung bình nhân là coi $\dfrac{1}{2}(x+y)$
là bán kính của một đường tròn và $\sqrt{xy}$ là đường cao xuất phát từ đỉnh góc vuông chắn nửa
đường tròn.
Ví dụ :
Từ một mảnh giấy bìa có dạng hình chữ nhật kích thước $15 \times 8 \ cm$, người ta cắt ra từ bốn góc của hình chữ nhật bốn hình vuông bằng nhau. Mảnh giấy còn lại trông giống như một chữ thập, được gấp làm một cái hộp (không nắp). Hỏi rằng cạnh của bốn hình vuông bằng bao nhiêu để thể tích của chiếc hộp thu được là lớn nhất.
Giải: Gọi $x$ là độ dài cạnh của hình vuông. Khi đó chiếc hộp sẽ có kích thước là $15-x-x; 8-x-x$ và $x$. Thể tích của chiếc hộp là $V$ được tính theo $x$ như sau
$$V = x(15-2x)(8-2x).$$
Ta cần tìm $x$ sao cho $V$ đạt giá trị lớn nhất. Khi chưa có công cụ đạo hàm, ta vẫn có thể tìm
giá trị lớn nhất của $V$ bằng cách sử dụng bất đẳng thức giữa trung bình cộng và trung bình
nhân.
Thực vậy, ta cần phải tìm $k,l$ trong $kx(15-2x)l(8-2x)$ sao cho
$$15-2x=l(8-2x)=kx,$$ và $$2+2l-k=0.$$
Từ đây, biểu diễn $x$ theo $k,l$ ta tìm $k,l$ bằng cách giải hệ phương trình
$$\dfrac{15-8l}{2(1-l)}=\dfrac{8l}{k+2l}$$
hay $2+2l-k=0.$
Giải hệ này cho ta $l=\dfrac{5}{2}, k = 7$. Bây giờ ta áp dụng bất đẳng thức giữa trung bình cộng và
trung bình nhân cho ba số,
$$
V=x(15-2x)(8-2x)=\dfrac{2}{35}.7x (15-2x)(20-5x)
\le \dfrac{2}{35} \left( \dfrac{7x+15-2x+20-5x}{3}\right)^3.
$$
Từ đó,
$$V \le \dfrac{2}{35}. \left(\dfrac{35}{3}\right)^3=\dfrac{2450}{27}.$$
Đẳng thức xảy ra khi và chỉ khi
$$7x=15-2x=20-5x.$$
Giải hệ phương trình này cho ta $x=\dfrac{5}{3}$. Vậy cạnh hình vuông là $\dfrac{5}{3}$ cm.
Bất đẳng thức giữa trung bình cộng và trung bình nhân
Với mọi số dương $a$ và $b$, ta luôn có
$$ \dfrac{a+b}{2} \, \geq \, \sqrt{ab} \, \geq \, \dfrac{2}{\dfrac{1}{a} + \dfrac{1}{b}}. \ \ \ (1.1)$$
Dấu bằng xảy ra khi và chỉ khi $a =b$.
Chứng minh:
Cách 1: Vì $a, b > 0$ nên ta có thể viết $a = x^2, b = y^2$ với $x, y > 0$. Ta có
$$
\dfrac{x^2 + y^2}{2} \geq xy.
$$
Điều này tương đương với
$$
(x-y)^2 \geq 0. \ \ \ (1.2)
$$
Rõ ràng, bất đẳng thức (1.2) luôn đúng với mọi $x, y$. Tức là, bất đẳng thức thứ nhất trong (1.1) được chứng minh. Chia bất đẳng thức này cho $ab$ ta nhận được
$$
\dfrac{\dfrac{a+b}{ab}}{2} \geq {\dfrac{\sqrt{ab}}{ab}} = \dfrac{1}{\sqrt{ab}}.
$$
Dễ dàng thấy rằng bất đẳng thức sau cùng này tương đương với bất đẳng thức thứ hai trong (1.1)
và dấu bằng trong (1.2) xảy ra khi và chỉ khi $x = y$.
Điều này có nghĩa là $a = b$ trong (1.1).
Cách 2: Bất đẳng thức (1.1) có thể được chứng minh bằng hình học như sau. Trước hết ta có
$$ \dfrac{2}{\dfrac{1}{a} + \dfrac{1}{b}} = \dfrac{2ab}{a+b}. $$
Ta viết lại bất đẳng thức (1.1) dưới dạng
$$ \dfrac{2ab}{a+b} \leq \sqrt{ab} \leq \dfrac{a+b}{2}. $$
Không hạn chế tổng quát, coi $a>b$. Dựng đường tròn tâm $A$ bán kính $\dfrac{a-b}{2}$ (như hình vẽ). Trên đường thẳng $Ax$ bất kì lấy điểm $M$ sao cho độ dài $AM = \dfrac{a+b}{2}$. Từ $M$ kẻ tiếp tuyến với đường tròn, gọi tiếp điểm là $G$. Từ $G$ kẻ $GH\bot Ax$. Sử dụng công thức Pythagoras cho tam giác vuông $AGM$ ta tính được độ dài các cạnh
$$ AM = \dfrac{a+b}{2}, \ GM =\sqrt{AM^2-AG^2}=\sqrt{\left(\dfrac{a+b}{2} \right)^2- \left(\dfrac{a-b}{2} \right)^2}= \sqrt{ab},
$$
$$ HM=\dfrac{GM^2}{AM}=\dfrac{ab}{\dfrac{a+b}{2}} = \dfrac{2ab}{a+b}. $$
Mặt khác, dựa vào tính chất của tam giác, ta có
$$ HM \leq GM \leq AM. $$
Suy ra
$$ \dfrac{2ab}{a+b} \leq \sqrt{ab} \leq \dfrac{a+b}{2}. $$
Nếu ta cho phép bán kính của đường tròn dần về 0, thì $G$ dần tới $A$, ta thu được dấu bằng trong bất đẳng thức trên.
$$ \dfrac{a+b}{2} \, \geq \, \sqrt{ab} \, \geq \, \dfrac{2}{\dfrac{1}{a} + \dfrac{1}{b}}. \ \ \ (1.1)$$
Dấu bằng xảy ra khi và chỉ khi $a =b$.
Chứng minh:
Cách 1: Vì $a, b > 0$ nên ta có thể viết $a = x^2, b = y^2$ với $x, y > 0$. Ta có
$$
\dfrac{x^2 + y^2}{2} \geq xy.
$$
Điều này tương đương với
$$
(x-y)^2 \geq 0. \ \ \ (1.2)
$$
Rõ ràng, bất đẳng thức (1.2) luôn đúng với mọi $x, y$. Tức là, bất đẳng thức thứ nhất trong (1.1) được chứng minh. Chia bất đẳng thức này cho $ab$ ta nhận được
$$
\dfrac{\dfrac{a+b}{ab}}{2} \geq {\dfrac{\sqrt{ab}}{ab}} = \dfrac{1}{\sqrt{ab}}.
$$
Dễ dàng thấy rằng bất đẳng thức sau cùng này tương đương với bất đẳng thức thứ hai trong (1.1)
và dấu bằng trong (1.2) xảy ra khi và chỉ khi $x = y$.
Điều này có nghĩa là $a = b$ trong (1.1).
Cách 2: Bất đẳng thức (1.1) có thể được chứng minh bằng hình học như sau. Trước hết ta có
$$ \dfrac{2}{\dfrac{1}{a} + \dfrac{1}{b}} = \dfrac{2ab}{a+b}. $$
Ta viết lại bất đẳng thức (1.1) dưới dạng
$$ \dfrac{2ab}{a+b} \leq \sqrt{ab} \leq \dfrac{a+b}{2}. $$
Không hạn chế tổng quát, coi $a>b$. Dựng đường tròn tâm $A$ bán kính $\dfrac{a-b}{2}$ (như hình vẽ). Trên đường thẳng $Ax$ bất kì lấy điểm $M$ sao cho độ dài $AM = \dfrac{a+b}{2}$. Từ $M$ kẻ tiếp tuyến với đường tròn, gọi tiếp điểm là $G$. Từ $G$ kẻ $GH\bot Ax$. Sử dụng công thức Pythagoras cho tam giác vuông $AGM$ ta tính được độ dài các cạnh
$$ AM = \dfrac{a+b}{2}, \ GM =\sqrt{AM^2-AG^2}=\sqrt{\left(\dfrac{a+b}{2} \right)^2- \left(\dfrac{a-b}{2} \right)^2}= \sqrt{ab},
$$
$$ HM=\dfrac{GM^2}{AM}=\dfrac{ab}{\dfrac{a+b}{2}} = \dfrac{2ab}{a+b}. $$
Mặt khác, dựa vào tính chất của tam giác, ta có
$$ HM \leq GM \leq AM. $$
Suy ra
$$ \dfrac{2ab}{a+b} \leq \sqrt{ab} \leq \dfrac{a+b}{2}. $$
Nếu ta cho phép bán kính của đường tròn dần về 0, thì $G$ dần tới $A$, ta thu được dấu bằng trong bất đẳng thức trên.
LƯỢNG GIÁC NÓI VỀ CÁI GÌ?
Từ lượng giác xuất hiện trong tiếng Hy Lạp có nghĩa là "đo đạc trong tam giác". Nó thành một nhánh của toán học dùng để tìm hiểu về tam giác và sự liên hệ giữa các cạnh của hình tam giác và các góc của nó. Vì vậy khi học về lượng giác bạn sẽ nghiên cứu nhiều hình tam giác đặc biệt là tam giác vuông.
Chúng ta xét xem một số ứng dụng của lượng giác trong đời sống hàng ngày:
Hôm nay có thể bạn sẽ nghe nhạc. Bài hát bạn nghe được ghi âm kĩ thuật số, được nén thành định dạng MP3 sử dụng nén giảm dữ liệu, phép nén này đòi hỏi các kiến thức về lượng giác.
Bạn đã bao giờ nhìn thấy cây cầu như này chưa?
Cây cầu được xây dựng bằng cách sử dụng các kiến thức lượng giác ở những góc khác nhau. Bạn sẽ nhận thấy cây cầu gồm nhiều hình tam giác- lượng giác đã được sử dụng khi thiết kế độ dài và độ vững chắc của những tam giác đó.
Hoặc như việc đo đạc một vật gì đó không thể đo trực tiếp bằng tay được, ví dụ như đo một cái cây hay một ngọn núi
Từ xưa người ta đã biết đo chiều cao của cái cây bằng cách sử dụng các hình tam giác tương ứng (như hình trên). Ta có thể dễ dàng có độ dài cạnh $AB$ và $AC$ của tam giác $ABC$, và cạnh $DB$ trong tam giác $DEB$. Sau đó ta dùng số liệu này để tìm chiều cao $DE$ (có thể tính thông qua $tan \hat B$ hoặc tam giác đồng dạng...). Ta có thể làm quá trình tương tự như tìm chiều cao của ngọn núi.
Lượng giác có rất nhiều ứng dụng trong các lĩnh vực: thiên văn, lý thuyết âm nhạc, âm học, quang học, y học, cơ khí, xây dựng....
Nguồn: http://diendantoanhoc.net/topic/149554-l%C6%B0%E1%BB%A3ng-gi%C3%A1c-n%C3%B3i-v%E1%BB%81-c%C3%A1i-g%C3%AC/
Chúng ta xét xem một số ứng dụng của lượng giác trong đời sống hàng ngày:
Hôm nay có thể bạn sẽ nghe nhạc. Bài hát bạn nghe được ghi âm kĩ thuật số, được nén thành định dạng MP3 sử dụng nén giảm dữ liệu, phép nén này đòi hỏi các kiến thức về lượng giác.
Bạn đã bao giờ nhìn thấy cây cầu như này chưa?
Cây cầu được xây dựng bằng cách sử dụng các kiến thức lượng giác ở những góc khác nhau. Bạn sẽ nhận thấy cây cầu gồm nhiều hình tam giác- lượng giác đã được sử dụng khi thiết kế độ dài và độ vững chắc của những tam giác đó.
Hoặc như việc đo đạc một vật gì đó không thể đo trực tiếp bằng tay được, ví dụ như đo một cái cây hay một ngọn núi
Từ xưa người ta đã biết đo chiều cao của cái cây bằng cách sử dụng các hình tam giác tương ứng (như hình trên). Ta có thể dễ dàng có độ dài cạnh $AB$ và $AC$ của tam giác $ABC$, và cạnh $DB$ trong tam giác $DEB$. Sau đó ta dùng số liệu này để tìm chiều cao $DE$ (có thể tính thông qua $tan \hat B$ hoặc tam giác đồng dạng...). Ta có thể làm quá trình tương tự như tìm chiều cao của ngọn núi.
Lượng giác có rất nhiều ứng dụng trong các lĩnh vực: thiên văn, lý thuyết âm nhạc, âm học, quang học, y học, cơ khí, xây dựng....
Nguồn: http://diendantoanhoc.net/topic/149554-l%C6%B0%E1%BB%A3ng-gi%C3%A1c-n%C3%B3i-v%E1%BB%81-c%C3%A1i-g%C3%AC/
TÍNH ĐỒNG BIẾN - NGHỊCH BIẾN CỦA HÀM SỐ
–o0o–
Định nghĩa :
Cho hàm số y = f(x) xác định trên D.
- khi giá trị của biến x tăng (giảm) trên D mà giá trị của hàm số tương ứng tăng (giảm). Ta gọi hàm số đồng biến trên D.
- khi giá trị của biến x tăng (giảm) trên D mà giá trị của hàm số tương ứng giảm (tăng). Ta gọi hàm số nghịch biến trên D.
Tóm tắt
Cho hàm số y = f(x) xác định trên D.
Hàm số được gọi là đồng biến trên D nếu :
Lấy x1, x2 ∈D sao cho : x1 < x2 => f(x1) < f(x2) .
Hàm số được gọi là nghịch biến trên D nếu :
x1, x2 ∈ D sao cho: x1 < x2 => f(x1) > f(x2) .
———————————-
Phương pháp :
Bước 1 : tìm tập xác định D.
Bước 2 : Lấy x1, x2 ∈ D sao cho : x1 < x2 => x2 – x1 > 0.
Bước 3 : tính : f(x1) = …
f(x2) = …
Bước 4 : so sánh f(x1) và f(x2) bằng cách :
xét hiệu : f(x2) – f(x1) = … (hoặc f(x2) : f(x1) = …).
- Nếu f(x1) < f(x2) : Hàm số được gọi là đồng biến trên D.
- Nếu f(x1) > f(x2) : Hàm số được gọi là nghịch biến trên D.
——————————–
Bài tập 1 Chứng minh rằng : hàm số y = f(x) = x + 1 đồng biến trên R.
giải:
TXĐ : D = R
Lấy x1, x2 ∈ D : x1 < x2 => x2 – x1 > 0.
tính : f(x1) = x1 + 1
f(x2) = x2 + 1
xét : f(x2) – f(x1) = (x2 + 1) – (x1 + 1) = x2 –x1
ta có : x2 – x1 > 0 => f(x2) – f(x1) > 0
=> f(x1) < f(x2)
Vậy : Hàm số đồng biến trên R.
Bài tập 2 : Chứng minh rằng : hàm số y = f(x) = -2x + 3 nghịch biến trên R.
giải:
TXĐ : D = R
Lấy x1, x2 ∈ D : x1 < x2 => x2 – x1 > 0.
tính : f(x1) = -2x1 + 3
f(x2) = -2x2 + 3
xét : f(x2) – f(x1) = (-2x2 + 3) – (-2x1 + 3) = -2(x2 –x1)
ta có : x2 – x1 > 0 => f(x2) – f(x1) < 0
=> f(x1) > f(x2)
Vậy : Hàm số nghịch biến trên R.
Bài tập 3 : Chứng minh rằng : hàm số y = f(x) = x2 – 5 nghịch biến trên khoảng ( -∞ ; 0) và đồng biến trên khoảng (0; +∞).
giải:
TXĐ : D = R
Lấy x1, x2 ∈ D : x1 < x2 => x2 – x1 > 0.
tính : f(x1) = x12 – 5
f(x2) = x22 – 5
xét : f(x2) – f(x1) = (x22 – 5) – (x12 – 5) = x22 – x12 = (x2 – x1) (x2 + x1)
Nếu x1, x2 ∈ ( -∞ ; 0) thì x2 + x1 < 0
ta lại có : x2 – x1 > 0 => (x2 – x1) (x2 + x1) < 0 => f(x2) – f(x1) < 0
=> f(x1) > f(x2)
Vậy : Hàm số nghịch biến trên khoảng ( -∞ ; 0).
Nếu x1, x2 ∈ (0; +∞) thì x2 + x1 > 0
ta lại có : x2 – x1 > 0 => (x2 – x1) (x2 + x1) > 0 => f(x2) – f(x1) > 0
=> f(x1) < f(x2)
Vậy : Hàm số đồng biến trên khoảng ( 0; +∞).
PHƯƠNG PHÁP XÉT TÍNH CHẴN - LẺ CỦA HÀM SỐ
–o0o—
Định nghĩa :
Hàm số y = f(x) với tập xác định D gọi là hàm số chẵn nếu :
x ∈ D thì -x ∈ D và f(-x) = f(x).
lưu ý : đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.
Hàm số y = f(x) với tập xác định D gọi là hàm số lẻ nếu :
x ∈ D thì -x ∈ D và f(-x) = -f(x).
lưu ý : đồ thị của hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
+ D là tập đối xứng có dạng : [-a; a] với a ∈ R.
————————–
Phương pháp :
Bước 1 : tìm TXĐ : D, chứng minh D là tập đối xứng.
Bước 2 : lấy x ∈ D => – x ∈ D.
Bước 3 : xét : f(-x) :
- Nếu f(-x) = … = f(x) : hàm số chẵn.
- Nếu f(-x) = … = – f(x) : hàm số lẻ.
- Nếu f(-x) = … ≠ – f(x) hoặc f(x): hàm số không chẵn, lẻ.
—————————-
Bài tập 1 : Xét tính chẵn lẻ của hàm số : y = f(x) = x3 + x.
TXĐ : D = R
=> D là tập đối xứng.
lấy x ∈ D => – x ∈ D.
Xét f(-x) = (-x)3 + (-x) = -( x3 + x)= -f(x)
=> f(-x) = – f(x).
Vậy hàm số y = x3 + x là hàm số lẻ.
Bài tập 2 : Xét tính chẵn lẻ của hàm số : y = f(x) = x4 + x2 – 2.
TXĐ : D = R
=> D là tập đối xứng.
lấy x ∈ D => – x ∈ D.
Xét : f(-x) = (-x)4 + (-x)2 – 2 = x4 + x2 – 2 = f(x)
=> f(-x) = f(x).
Vậy hàm số y = x4 + x2 – 2 là hàm số chẵn.
Bài tập 3 : Xét tính chẵn lẻ của hàm số : y = f(x) =  – 5.
– 5.
TXĐ : 2x + 8 ≥ 0 <=> x ≥ – 4
D = [-4; + ∞)
ta có : 5 ∈ D mà – 5 ∉ D => D không là tập đối xứng.
Vậy hàm số không chẵn, không lẻ.
Bài tập 4 : Xét tính chẵn lẻ của hàm số : y = f(x) = 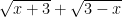 .
.
Đk :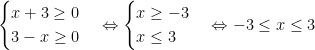
Vậy : D = [-3; 3] : miền đối xứng.
lấy x ∈ D => – x ∈ D.
Xét : f(-x) =  = f(x)
= f(x)
=> f(-x) = f(x)
Vậy hàm số y = 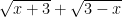 là hàm số chẵn.
là hàm số chẵn.
Bài tập rèn luyện : Xét tính chẵn – lẻ của các hàm số sau :
TỔNG HỢP HỆ PHƯƠNG TRÌNH (CÓ ĐÁP ÁN)
Chuyên đề là kết quả thu được qua một thời gian học tập và nghiên cứu của bản thân về hệ phương trình. Tuy nhiên có thể nói rằng, đó là sự kết tinh qua nhiều thế hệ, là sự giúp đỡ, là sự học hỏi từ những người bạn của mình cũng như rất nhiều yếu tố khác.
Để đạt hiệu quả cao khi tham khảo chuyên đề này, xin được trích dẫn mấy lời của nhà giáo G.Polya:
" [...] Một số bài toán có nêu lời giải đầy đủ (tuy vắn tắt), đối với một số bài khác, chỉ vạch ra mấy bước giải đầu tiên, và đôi khi chỉ đưa ra kết quả cuối cùng"
Một số bài toán có kèm thêm chỉ dẫn để giúp người đọc giải được dễ dàng hơn. Chỉ dẫn cũng có thể nằm trong những bài toán khác ở gần bài toán đang xét. Nên đặc biệt lưu ý đến những nhận xét mở đầu trước từng bài tập hay cả một nhóm bài tập gặp thấy trong chương.
Nếu chịu khó, gắng sức giải một bài toán nào đó thì dù không giải nổi đi chăng nữa, bạn đọc cũng thu hoạch được nhiều điều bổ ích. Chẳng hạn, bạn đọc có thể giở ra xem (ở cuốn sách) phần đầu mỗi lời giải, đem đối chiếu với những suy nghĩ của bản thân mình, rồi gấp sách lại và thử gắng tự lực tìm ra phần còn lại của lời giải.
Có lẽ thời gian tốt nhất để suy nghĩ, nghiền ngẫm về phương pháp giải bài toán là lúc bạn vừa tự lực giải xong bài toán hay vừa đọc xong lời giải bài toán trong sách, hay đọc xong phần trình bày phương pháp giải trong sách. Khi vừa hoàn thành xong nhiệm vụ, và các ấn tượng hãy còn "nóng hổi", nhìn lại những nổ lực vừa qua của mình, bạn đọc có thể phân tích sâu sắc tính chất của những khó khăn đã vượt qua. Bạn đọc đọc có thể tự đặt cho mình nhiều câu hỏi bổ ích: "Khâu nào trong quá trình giải là quan trọng nhất? Khó khăn chủ yếu là ở chỗ nào? Ta có thể làm gì cho tốt hơn? Chi tiết ấy mình cũng đã liếc qua mà không chú ý đến - muốn "nhìn thấy" chi tiết này thì đầu óc phải có tư chất ra sao? Liệu ở đây có một cách gì đó đáng lưu ý để sau này gặp một tình huống tương tự, ta có thể áp dụng được không?" Tất cả những câu hỏi đó đều hay cả, và cũng còn nhiều câu hỏi bổ ích khác nữa, nhưng câu hỏi hay nhất chính là câu hỏi tự nhiên nảy ra trong óc, không cần ai gợi ý cả!"
https://dl.dropboxusercontent.com/content_link/NXXRjVN25Ya5y1NMg2pJc0R8T2YfBpFFqImIdPhbFkisZaZBkPCyUrMvbCASP4D9/file
(trích "Mấy lời khuyên và chỉ dẫn" -G.Polya trong "Sáng tạo toán học
Để đạt hiệu quả cao khi tham khảo chuyên đề này, xin được trích dẫn mấy lời của nhà giáo G.Polya:
" [...] Một số bài toán có nêu lời giải đầy đủ (tuy vắn tắt), đối với một số bài khác, chỉ vạch ra mấy bước giải đầu tiên, và đôi khi chỉ đưa ra kết quả cuối cùng"
Một số bài toán có kèm thêm chỉ dẫn để giúp người đọc giải được dễ dàng hơn. Chỉ dẫn cũng có thể nằm trong những bài toán khác ở gần bài toán đang xét. Nên đặc biệt lưu ý đến những nhận xét mở đầu trước từng bài tập hay cả một nhóm bài tập gặp thấy trong chương.
Nếu chịu khó, gắng sức giải một bài toán nào đó thì dù không giải nổi đi chăng nữa, bạn đọc cũng thu hoạch được nhiều điều bổ ích. Chẳng hạn, bạn đọc có thể giở ra xem (ở cuốn sách) phần đầu mỗi lời giải, đem đối chiếu với những suy nghĩ của bản thân mình, rồi gấp sách lại và thử gắng tự lực tìm ra phần còn lại của lời giải.
Có lẽ thời gian tốt nhất để suy nghĩ, nghiền ngẫm về phương pháp giải bài toán là lúc bạn vừa tự lực giải xong bài toán hay vừa đọc xong lời giải bài toán trong sách, hay đọc xong phần trình bày phương pháp giải trong sách. Khi vừa hoàn thành xong nhiệm vụ, và các ấn tượng hãy còn "nóng hổi", nhìn lại những nổ lực vừa qua của mình, bạn đọc có thể phân tích sâu sắc tính chất của những khó khăn đã vượt qua. Bạn đọc đọc có thể tự đặt cho mình nhiều câu hỏi bổ ích: "Khâu nào trong quá trình giải là quan trọng nhất? Khó khăn chủ yếu là ở chỗ nào? Ta có thể làm gì cho tốt hơn? Chi tiết ấy mình cũng đã liếc qua mà không chú ý đến - muốn "nhìn thấy" chi tiết này thì đầu óc phải có tư chất ra sao? Liệu ở đây có một cách gì đó đáng lưu ý để sau này gặp một tình huống tương tự, ta có thể áp dụng được không?" Tất cả những câu hỏi đó đều hay cả, và cũng còn nhiều câu hỏi bổ ích khác nữa, nhưng câu hỏi hay nhất chính là câu hỏi tự nhiên nảy ra trong óc, không cần ai gợi ý cả!"
https://dl.dropboxusercontent.com/content_link/NXXRjVN25Ya5y1NMg2pJc0R8T2YfBpFFqImIdPhbFkisZaZBkPCyUrMvbCASP4D9/file
(trích "Mấy lời khuyên và chỉ dẫn" -G.Polya trong "Sáng tạo toán học
TOÀN BỘ CÔNG THỨC TOÁN THPT3-ĐẠO HÀM-TÍCH PHÂN-NHỊ THỨC NEWTON
Phần III. ĐẠO HÀM – TÍCH PHÂN – HÌNH HỌC – NHỊ THỨC NEWTON
1. Đạo hàm
2. Bảng các nguyên hàm
3. Diện tích hình phẳng – Thể tích vật thể tròn xoay
4. Phương pháp tọa độ trong mặt phẳng
5. Phương pháp tọa độ trong không gian
6. Nhị thức Newton
2. Bảng các nguyên hàm
3. Diện tích hình phẳng – Thể tích vật thể tròn xoay
4. Phương pháp tọa độ trong mặt phẳng
5. Phương pháp tọa độ trong không gian
6. Nhị thức Newton
Chúc các em học tập tốt!
TOÀN BỘ CÔNG THỨC TOÁN THPT2-LƯỢNG GIÁC
Bao gồm 3 chuyên đề lớn
1. Công thức lượng giác
2. Phương trình lượng giác
TOÀN BỘ CÔNG THỨC THOÁN THPT1
PHẦN I: ĐẠI SỐ
1. Tam thức bậc 2
2. Bất đẳng thức Cauchy
3. Cấp số cộng
4. Cấp số nhân
5. Phương trình, bất phương trình chứa giá trị tuyệt đối
6. Phương trình, bất phương trình chứa căn
7. Phương trình, bất phương trình logarit
8. Phương trình, bất phương trình mũ
9. Lũy thừa
2. Bất đẳng thức Cauchy
3. Cấp số cộng
4. Cấp số nhân
5. Phương trình, bất phương trình chứa giá trị tuyệt đối
6. Phương trình, bất phương trình chứa căn
7. Phương trình, bất phương trình logarit
8. Phương trình, bất phương trình mũ
9. Lũy thừa
10. Logarit
CÔNG THỨC TOÁN THCS-THPT
Unknown
11:02
TOÁN HỌC 10
,
TOÁN HỌC 11
,
TOÁN HỌC 12
,
TOÁN HỌC 8
,
TOÁN HỌC 9
,
TOÁN THCS
,
TOÁN THPT
Bình luận
Bảng công thức gồm có 33 điều cần nhớ. Mỗi phần nhớ này là của 1 chương trình học khác nhau có đầy đủ từ đại số đến hình học.