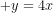Ta có:
1) Hàm số có hai cực trị ( có cực trị) khi và chỉ khi phương trình
2) Hàm số có hai cực trị trái dấu khi và chỉ khi đồ thị hàm số cắt Ox tại ba điểm phân biệt.
3) Hàm số đạt cực đại (cực tiểu) tại
Cách tính cực trị hàm số bậc ba:
Cách 1: Nếu hai nghiệm
Cách 2: Nếu hai nghiệm
Ví dụ 1. Tìm tất cả các giá trị của tham số
1)
2)
3)
Lời giải.
1) Ta có:
Hàm số có hai điểm cực trị
Hay
Khi đó:
Kết hợp với (a) ta có
2) TXĐ:
Ta có:
Hàm số có hai điểm cực trị nhỏ hơn
Bằng cách xét hàm số
Do đó
Vậy
3) Ta có:
Hàm số có hai điểm cực trị
(1) có hai nghiệm
Khi đó theo định lí Viet, ta có:
Suy ra
Từ đó ta tìm được
Vậy
Ví dụ 2. Tìm tất cả các giá trị của tham số
1)
2)
3)
Lời giải.
1) Ta có
Hàm số có cực đại và cực tiều khi và chỉ khi
Gọi
Điểm
Vậy
2) TXĐ:
Ta có
Suy ra
Do đó:
Nên
Vì ta phải có
Vậy
3) Ta có:
Đồ thị hàm số có hai điểm cực trị A, B khi và chỉ khi
Phương trình
Do đó
Kết hợp với điều kiện
Ví dụ 3. Tìm
Lời giải.
Ta có
Suy ra
Hàm số có hai cực trị khi và chỉ khi phương trình (1) có hai nghiệm phân biệt
Chia
Do đó, hai cực trị của hàm số trái dấu khi và chỉ khi
Vậy
Bài tập
Bài 1. Tìm tất cả các giá trị của tham số  để hàm số:
để hàm số:
1) (%7B%7Bx%7D%5E%7B2%7D%7D-3x-m-1)) có hai điểm cực trị
có hai điểm cực trị  thỏa
thỏa 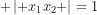 .
.
ĐS: 
2) %7B%7Bx%7D%5E%7B2%7D%7D+6(m-2)x+2) đạt cực trị tại
đạt cực trị tại  thỏa
thỏa 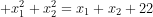 .
.
ĐS: 
3) x) có hai điểm cực trị
có hai điểm cực trị  là hai cạnh góc vuông của tam giác vuông có cạnh huyền bằng
là hai cạnh góc vuông của tam giác vuông có cạnh huyền bằng  .
.
ĐS: 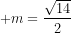 .
.
4) %7B%7Bx%7D%5E%7B2%7D%7D-%5Cleft(+3%7B%7Bm%7D%5E%7B2%7D%7D+7m-1+%5Cright)x+%7B%7Bm%7D%5E%7B2%7D%7D-1) đạt cực tiểu tại điểm nhỏ hơn 1.
đạt cực tiểu tại điểm nhỏ hơn 1.
ĐS: 
5) x-%7B%7Bm%7D%5E%7B2%7D%7D) đạt cực trị tại
đạt cực trị tại  thỏa
thỏa 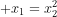 .
.
ĐS: 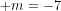
Bài 2. Tìm tất cả các giá trị của tham số  để hàm số
để hàm số
1) %7B%7Bx%7D%5E%7B2%7D%7D+12mx-20m+13) có hai cực trị lớn hơn
có hai cực trị lớn hơn  .
.
ĐS: 
2) x-2m+1) có hai cực trị cùng dấu.
có hai cực trị cùng dấu.
ĐS: $$\left\{ \begin{matrix} & m\ne 1 \\ & \frac{1}{2} < m < 3 \\ \end{matrix} \right.$$
Bài 3.Tìm tất cả các giá trị của tham số  để đồ thị hàm số:
để đồ thị hàm số:
1) 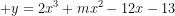 có hai điểm cực trị cách đều trục tung.
có hai điểm cực trị cách đều trục tung.
ĐS: 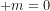
2) 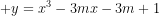 có hai điểm cực trị cách đều đường thẳng
có hai điểm cực trị cách đều đường thẳng 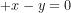 .
.
ĐS: 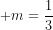
3) %7B%7Bx%7D%5E%7B2%7D%7D+6m(1-2m)x) có các điểm cực trị nằm trên đường thẳng
có các điểm cực trị nằm trên đường thẳng